안녕하세요~
오늘 이 시간에는 그래프에 대해서 알아볼까 합니다.
음 그래프란 무엇일까요?
그래프란 유한 개의 정점(V(G))과 유한개의 간선(E(G)) 구성된 집합입니다.
간선의 집합은 공집합일수도 있습니다. 즉 정점의 경우 하나도 존재하지 않는 그래프는 없지만 간선이 존재하지 않는 그래프는 존재할 수 있습니다.
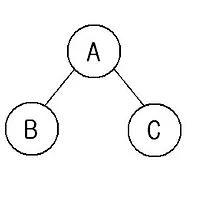
 예를 들어 이런 그래프가 있다고 한다면 각각의 점이라고 할수 있는 A, B, C, D는 정점이고,
예를 들어 이런 그래프가 있다고 한다면 각각의 점이라고 할수 있는 A, B, C, D는 정점이고,
이의 연결선이 간선입니다.
V(G) = {A, B, C, D}
E(G) = {(A,B), (A,C), (A,D), (B,D), (C,D)}
라고 할 수 있습니다.

또한 왼쪽의 경우 그래프라 할 수 있지만 오른쪽은 그래프라 할 수 없는것이지요.
그래프에는 방향성을 가지느냐 가지지 않느냐로 방향성 그래프(directed graph)와
무방향성 그래프(undirected graph) 두 가지로 나누어 집니다.

왼쪽이 무방향 그래프입니다. 간선에 방향성이 없지요? 이렇듯 두개의 정점을 연결하는 간선들에 방향성이 없는것을 무방향 그래프라고 합니다. 이때 (A,B)와 (B,A)는 같은 간선을 표현했다고 할 수 있습니다.
집합으로 표현하자면
V(G) = {A, B, C, D}
E(G) = {(A,B), (A,C), (A,D), (B,D), (C,D)}
가 될 수 있겠죠?
오른쪽의 경우를 볼까요? 네 화살표가 있네요. 이렇게 방향을 가지고 있는 그래프를 방향성 그래프라고 합니다.
이렇게 방향을 가진 그래프를 집합으로 표현할 때 ()가 아닌 <>를 사용합니다.
V(G) = {A, B, C, D}
E(G) = {<A,B>, <A,C>, <A,D>, <B,D>, <D,C>}
라고 표현합니다. 처음부분은 출발하는 정점, 뒤에는 도착하는 정점을 표현합니다.
또 그래프에는 루프(self loop)라는 것이 있습니다.
그냥 어떠한 정점에서 나와서 다시 그 정점으로 들어가는 간선을 말합니다.
 이런것을 말이지요. 왼쪽의 경우 무방향성이므로 (A,A)이고 오른쪽은 방향성이므로 <A,A>라고 해야 겠지요?
이런것을 말이지요. 왼쪽의 경우 무방향성이므로 (A,A)이고 오른쪽은 방향성이므로 <A,A>라고 해야 겠지요?
그래프에는 완전그래프(complete graph)와 부분그래프(subgraph)라는 것이 있습니다.
완전그래프라는것은 이름에서 느껴지듯이 모든 정점이 다른 모든 정점으로 간선이 이어져 있는것을 말합니다.

위에 그림을 볼까요? 처음 그래프는 정점이 하나인 그래프이군요. 연결될 다른 정점이 없으니 간선은 없네요
두번째 그래프는 정점이 두개가 있군요. 이러면 그 둘의 정점을 이을 간선이 하나 존재하겠네요.
세번째그래프는 어떤가요? 세개의 정점을 모두 이어야 하므로 3개, 네번째그래프는 네개의 정점을 잇는 6개의
간선들이 존재하는군요. 정점의 갯수를 n이라고 할때, 완전그래프의 간선의 개수는 n(n-1)/2 이겠지요?
아 이건 무방향 그래프이지요?
방향 그래프라면 A라는 정점에서 B라는 정점으로 가는 간선과 B라는 정점에서 A라는 정점으로 가는 간선이 존재하므로 2개의 간선이 생기지요? 때문에 무방향 그래프보다 2개의 간선의 개수를 가지므로 n(n-1)이 되겠군요.
부분그래프를 N이라 하면 완전그래프 G에 대해서 V(N)⊆V(G) 이고 E(N)⊆E(G)인 그래프를 말합니다.
즉 완전그래프의 부분집합인 그래프인 것이지요.
그래프에 인접하다(adjacent)와 부속하다(incident)라는 말이 있습니다.
인접하다라는 것은 간선으로 이어진 정점들을 인접하다라고 합니다.
만약 간선이 (A,B)라고 한다면 A와 B는 인접한다고 할 수 있는것이지요.
부속하다라는 것은 정점에 이어져있는 간선들은 그 정점에 부속한다고 할 수 있는것입니다.
아까 예를 들었던 간선(A,B)는 정점 A와 B의 부속한다고 할 수 있습니다.
마지막으로 차수(degree)라는 것이 있습니다.
차수라는 것은 어떤 정점에 부속되어있는 간선의 개수를 차수라고 합니다.
 이런 그래프가 있다고 해보지요. 왼쪽의 무방향성 그래프의 정점 A의 차수는 몇일까요?
이런 그래프가 있다고 해보지요. 왼쪽의 무방향성 그래프의 정점 A의 차수는 몇일까요?
A를 보시면 3개의 간선과 만나고 있지요?
왜 간선은 2개인데 3개랑 만나고 있다고 하냐고 궁금해 하실수도 있겠군요.
루프의 경우 두 부분 모두 A와 만나고 있기 때문이지요.
이렇게 루프의 경우 2개로 셉니다. 그러므로 왼쪽의 경우 A의 차수는 3입니다.
그럼 오른쪽의 방향성 그래프를 볼까요?
방향성 그래프는 무방향성과 다르게 진입차수(indegree)와 진출차수(outdegree)라는 것이 있습니다.
진입차수는 이름대로 그 정점으로 들어오는 즉 화살표의 촉 방향을 말합니다.
진출차수는 반대로 정점에서 시작하는 즉 화살표가 시작하는 부분인 것이지요.
그럼 오른쪽의 방향성 그래프의 정점 A의 차수를 세볼까요?
우선 진입차수는 A에 루프에서 오는 촉이 하나가 있으므로 1이고,
진출차수는 루프의 시작부분과 B로 향하는 화살표 총 2개가 있으므로 2가 되겠지요.
음 오늘은 그래프에 대하여 글을 써봤는데요.
고칠 부분이나 빠진 부분이 있으면 알려주시길 빌게요~
오늘 이 시간에는 그래프에 대해서 알아볼까 합니다.
음 그래프란 무엇일까요?
그래프란 유한 개의 정점(V(G))과 유한개의 간선(E(G)) 구성된 집합입니다.
간선의 집합은 공집합일수도 있습니다. 즉 정점의 경우 하나도 존재하지 않는 그래프는 없지만 간선이 존재하지 않는 그래프는 존재할 수 있습니다.

이의 연결선이 간선입니다.
V(G) = {A, B, C, D}
E(G) = {(A,B), (A,C), (A,D), (B,D), (C,D)}
라고 할 수 있습니다.

또한 왼쪽의 경우 그래프라 할 수 있지만 오른쪽은 그래프라 할 수 없는것이지요.
그래프에는 방향성을 가지느냐 가지지 않느냐로 방향성 그래프(directed graph)와
무방향성 그래프(undirected graph) 두 가지로 나누어 집니다.

왼쪽이 무방향 그래프입니다. 간선에 방향성이 없지요? 이렇듯 두개의 정점을 연결하는 간선들에 방향성이 없는것을 무방향 그래프라고 합니다. 이때 (A,B)와 (B,A)는 같은 간선을 표현했다고 할 수 있습니다.
집합으로 표현하자면
V(G) = {A, B, C, D}
E(G) = {(A,B), (A,C), (A,D), (B,D), (C,D)}
가 될 수 있겠죠?
오른쪽의 경우를 볼까요? 네 화살표가 있네요. 이렇게 방향을 가지고 있는 그래프를 방향성 그래프라고 합니다.
이렇게 방향을 가진 그래프를 집합으로 표현할 때 ()가 아닌 <>를 사용합니다.
V(G) = {A, B, C, D}
E(G) = {<A,B>, <A,C>, <A,D>, <B,D>, <D,C>}
라고 표현합니다. 처음부분은 출발하는 정점, 뒤에는 도착하는 정점을 표현합니다.
또 그래프에는 루프(self loop)라는 것이 있습니다.
그냥 어떠한 정점에서 나와서 다시 그 정점으로 들어가는 간선을 말합니다.

그래프에는 완전그래프(complete graph)와 부분그래프(subgraph)라는 것이 있습니다.
완전그래프라는것은 이름에서 느껴지듯이 모든 정점이 다른 모든 정점으로 간선이 이어져 있는것을 말합니다.

위에 그림을 볼까요? 처음 그래프는 정점이 하나인 그래프이군요. 연결될 다른 정점이 없으니 간선은 없네요
두번째 그래프는 정점이 두개가 있군요. 이러면 그 둘의 정점을 이을 간선이 하나 존재하겠네요.
세번째그래프는 어떤가요? 세개의 정점을 모두 이어야 하므로 3개, 네번째그래프는 네개의 정점을 잇는 6개의
간선들이 존재하는군요. 정점의 갯수를 n이라고 할때, 완전그래프의 간선의 개수는 n(n-1)/2 이겠지요?
아 이건 무방향 그래프이지요?
방향 그래프라면 A라는 정점에서 B라는 정점으로 가는 간선과 B라는 정점에서 A라는 정점으로 가는 간선이 존재하므로 2개의 간선이 생기지요? 때문에 무방향 그래프보다 2개의 간선의 개수를 가지므로 n(n-1)이 되겠군요.
부분그래프를 N이라 하면 완전그래프 G에 대해서 V(N)⊆V(G) 이고 E(N)⊆E(G)인 그래프를 말합니다.
즉 완전그래프의 부분집합인 그래프인 것이지요.
그래프에 인접하다(adjacent)와 부속하다(incident)라는 말이 있습니다.
인접하다라는 것은 간선으로 이어진 정점들을 인접하다라고 합니다.
만약 간선이 (A,B)라고 한다면 A와 B는 인접한다고 할 수 있는것이지요.
부속하다라는 것은 정점에 이어져있는 간선들은 그 정점에 부속한다고 할 수 있는것입니다.
아까 예를 들었던 간선(A,B)는 정점 A와 B의 부속한다고 할 수 있습니다.
마지막으로 차수(degree)라는 것이 있습니다.
차수라는 것은 어떤 정점에 부속되어있는 간선의 개수를 차수라고 합니다.

A를 보시면 3개의 간선과 만나고 있지요?
왜 간선은 2개인데 3개랑 만나고 있다고 하냐고 궁금해 하실수도 있겠군요.
루프의 경우 두 부분 모두 A와 만나고 있기 때문이지요.
이렇게 루프의 경우 2개로 셉니다. 그러므로 왼쪽의 경우 A의 차수는 3입니다.
그럼 오른쪽의 방향성 그래프를 볼까요?
방향성 그래프는 무방향성과 다르게 진입차수(indegree)와 진출차수(outdegree)라는 것이 있습니다.
진입차수는 이름대로 그 정점으로 들어오는 즉 화살표의 촉 방향을 말합니다.
진출차수는 반대로 정점에서 시작하는 즉 화살표가 시작하는 부분인 것이지요.
그럼 오른쪽의 방향성 그래프의 정점 A의 차수를 세볼까요?
우선 진입차수는 A에 루프에서 오는 촉이 하나가 있으므로 1이고,
진출차수는 루프의 시작부분과 B로 향하는 화살표 총 2개가 있으므로 2가 되겠지요.
음 오늘은 그래프에 대하여 글을 써봤는데요.
고칠 부분이나 빠진 부분이 있으면 알려주시길 빌게요~
'(탈퇴) 테슬라's Post' 카테고리의 다른 글
| 그래프(Graph) - 표현법?? (0) | 2009.02.05 |
|---|---|
| Tesla's Post 연기 됩니다. (0) | 2009.01.25 |
| Tesla's post 연기 공지 (0) | 2009.01.19 |
| 이진 트리(Binary Tree) - 이진 트리의 운행 2 (5) | 2009.01.06 |
| 이진 트리(Binary Tree) - 이진 트리의 운행 1 (6) | 2008.12.30 |