Red-Black Tree 두 번째 포스트입니다.
이번엔 Red-Black Tree 의 회전에 대해서 알아볼까요.
앞서 Red-Black Tree 의 유지조건에 대해 언급드렸을 겁니다.
Introduction to Algorithms 의 Red-Black Tree 절에 따르면 다음과 같은 정의가 성립해야 하죠.
1. Every node is either red or black.
모든 node 는 적색 혹은 흑색이다.
2. The root is black.
root 는 흑색이다.
3. Every leaf is black.
모든 leaf 는 흑색이다.
4. If a node is red, then both its children are black.
만약 한 node 가 적색이라면, 이 node 의 두 자식은 모두 흑색이다.
5. For each node, all paths from the node to descendant leaves contain the same number of black nodes.
각 node 로부터, node 에서 자손까지의 모든 경로들은 같은 갯수의 흑색 node 를 포함한다(가진다).
만약 한 레코드 셋에 새로운 값이 삽입된다고 가정해 봅시다.모든 node 는 적색 혹은 흑색이다.
2. The root is black.
root 는 흑색이다.
3. Every leaf is black.
모든 leaf 는 흑색이다.
4. If a node is red, then both its children are black.
만약 한 node 가 적색이라면, 이 node 의 두 자식은 모두 흑색이다.
5. For each node, all paths from the node to descendant leaves contain the same number of black nodes.
각 node 로부터, node 에서 자손까지의 모든 경로들은 같은 갯수의 흑색 node 를 포함한다(가진다).
그러면 Red-Black Tree 의 성질이 유지될 수 있을까요?
물론 유지될 수도 있습니다.
하지만, 모든 경우에 대한 것은 아니지요. 즉, 유지되지 않는 경우가 생긴다는 말입니다.
레코드 셋에 대한 검색 알고리즘들은 모두 이런 경우를 대비해 삽입 . 삭제 기능을 같이 갖추어야 합니다.
사용자가 레코드 셋을 언제 수정할 지 모르니까요.
그리고 이 알고리즘의 특성을 유지시키기 위한 방법 역시 요구합니다.
애써 구축해 놓은 레코드 셋의 구조가 엉켜버리면 곤란하겠죠.
즉, 아무리 빠르고 강력한 알고리즘이라 할지라도 그 알고리즘의 특성을 유지시키기 위한 프로시저는 반드시
존재해야 한다는 것이죠.
Red-Black Tree 는 사용자에 의해 레코드 셋이 수정될 때마다 rotation - 회전 - 을 수행합니다.
앞서 Red-Black Tree 는 Binary Search Tree 의 일종이라는 말씀을 드렸을 겁니다.
그럼 우선 Binary Tree 의 rotation 연산을 살펴볼까요.
rotation 연산은 2개가 있습니다.
짐작하시다시피 Left Rotation, Right Rotation 이죠.
우선 Left Rotation 부터 볼까요. 다음의 그림을 기준으로 하여 설명합니다.
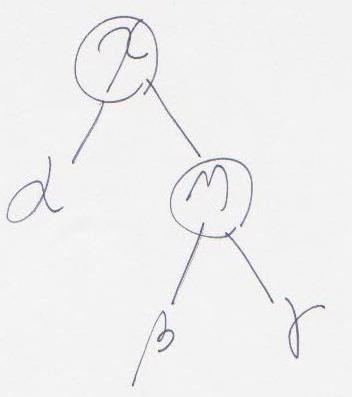
Left Rotation.
1. y 의 왼쪽 sub tree 를 x 의 오른쪽 sub tree 로 옮긴 뒤, x 와 y 의 관계를 끊는다.
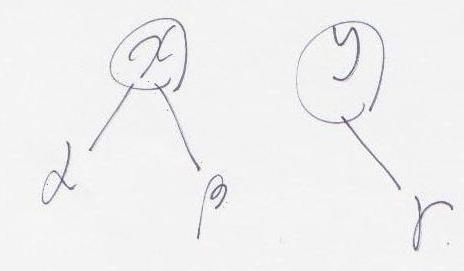 2. x tree 를 y 의 왼쪽 자손으로 삼는다.
2. x tree 를 y 의 왼쪽 자손으로 삼는다.
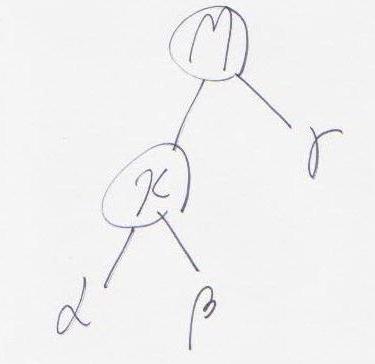
1. y 의 왼쪽 sub tree 를 x 의 오른쪽 sub tree 로 옮긴 뒤, x 와 y 의 관계를 끊는다.


Right Rotation 은 Left Rotation 의 역순으로 생각하시면 됩니다.
-사실, 위에서 설명드린 방식은 정석에서 살짝 벗어난 설명입니다.
하지만 개인적으로는 저렇게 이해하고 있고 -_- 이해도 편하기에 저렇게 설명드렸습니다.
특히 관계를 끊는다는 부분에서 말이죠. -_- -
rotaion 연산은 단지 추상화가 저렇게 될 뿐, 실제 코딩에서는 단순 포인터 연산으로 구현되므로 상수시간 안에
실행될 수 있습니다.
주로 Red - Black Tree 의 삽입 프로시저에서 Left Rotation, Right Rotation 을 실행하는 형식으로 실행되곤 하죠.
결국 오늘 다 못끝냈군요 -_-;;;
다음 포스트에서는 삽입, 삭제 연산을 다루고 Red-Black Tree 의 포스트를 마쳐보겠습니다.
'(탈퇴) Reuent's Post > Algorithms' 카테고리의 다른 글
| Algorithm #2. Search algorithm. - 2.5 Red-Black Tree (1). (0) | 2010.03.04 |
|---|---|
| Algorithm #2. Search algorithm. - 2.4 Binary Tree Search (2). (0) | 2010.03.04 |
| Algorithm #2. Search algorithm. - 2.4 Binary Tree Search (1). (0) | 2010.03.04 |
| Algorithm #2. Search algorithm. - 2.3 Binary Search. (1) | 2010.03.04 |
| Algorithm #2. Search algorithm. - 2.2 Sequential Search. (0) | 2010.03.04 |