안녕하십니까 Mr. K입니다
다들 이번 문제에 대해 혼란스러워하는 것 같아서 일단 제가 해석한 대로 전개해보겠습니다
친구와 약간의 음주를 하고 와서 쓰는 것이라 약간 말이 안되어보이는 것이 있을지도 모르겠습니다만 그냥 쓰겠습니다
문제의 입력 예시를 보면
4
2 1 2
2 1 2
2 2 3
2 3 4
1 2 3 4
라고 되어있는데,
여기서 마지막줄의 "1 2 3 4", 즉 '마법사가 만들었던 원래의 결과물'은 무시하기로 합니다
(왜 우리가 output으로 나와야 하는 한가지 경우의 수를 input으로 넣어야 하는지에 대한 의문도 잠시 접어두기로 하고)
그리고나서
2 1 2
2 1 2
2 2 3
2 3 4
를 보면,
첫번째 왕자는 2명의 소녀를 좋아하고, 그 소녀의 번호는 각각 1과 2입니다
두번째 왕자는 2명의 소녀를 좋아하고, 그 소녀의 번호는 각각 1과 2입니다
세번째 왕자는 2명의 소녀를 좋아하고, 그 소녀의 번호는 각각 2와 3입니다
네번째 왕자는 2명의 소녀를 좋아하고, 그 소녀의 번호는 각각 3과 4입니다
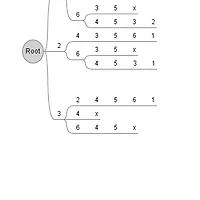
이것을 표로 그리면 아래와 같은데요

문제가 요구하는 것이 무엇인고 하니,
왕자(B)와 소녀(G)가 겹치지 않도록 일대일로 짝을 지어주는 모든 경우를 세고,
어느 왕자도 결혼하지 않은 상태를 가정하고 각 왕자가 다른 왕자의 결혼을 방해하지 않도록 선택할 수 있는 소녀를 모두 나열하는 것입니다
말이 좀 어려운데,
문제에 나온 예시를 먼저 보도록 하죠
위의 표를 참고해도 좋습니다
우선, 1번 왕자와 1번 소녀를 결혼시킵니다
그러면 2번 왕자는 1번 왕자와 같은 소녀를 고르면 안되므로 2번 소녀와 결혼시킵니다
그러면 3번 왕자는 1,2번 왕자와 같은 소녀를 고르면 안되므로 3번 소녀와 결혼시킵니다
마찬가지로 4번 왕자는 1~3번 왕자와 같은 소녀를 고르면 안되므로 4번 소녀와 결혼시킵니다
그러면 (1, 1) - (2, 2) - (3, 3) - (4, 4) 와 같은 한가지 경우가 만들어집니다
그런데 1번 왕자는 2번 소녀도 좋아하므로 위에서 했던 작업은 다 잊어버리고,
1번 왕자와 2번 소녀를 결혼시킵니다
2번 왕자는 1번 왕자와 같은 소녀를 고르면 안되므로 1번 소녀와 결혼시킵니다
그러면 3번 왕자는 1, 2번 왕자와 같은 소녀를 고르면 안되므로 3번 소녀와 결혼시킵니다
그리고 4번 왕자는 1~3번 왕자와 같은 소녀를 고르면 안되므로 4번 소녀와 결혼시킵니다
그러면 (1, 2) - (2, 1) - (3, 3) - (4, 4) 와 같은 한가지 경우가 만들어집니다
이 결과를 정리해보면,
어느 왕자도 결혼하지 않은 상태를 가정했을 때,
1번 왕자는 1번 소녀나 2번 소녀를 선택할 수 있습니다
2번 왕자도 1번 소녀나 2번 소녀를 선택할 수 있습니다
3번 왕자는 3번 소녀만을 선택할 수 있습니다
4번 왕자는 4번 소녀만을 선택할 수 있습니다
그래서 출력 예시에
2 1 2
2 1 2
1 3
1 4
가 나오는 것이 아닐까 생각해봅니다
이 문제를 풀면서 혼자 만들어본 케이스가 2개 더 있습니다
두번째 케이스입니다

이번에도 역시
1번 왕자를 1번 소녀와 결혼시킵니다
이 때, 2번 왕자는 2번 소녀와 3번 소녀 모두와 결혼할 수 있는데, 3번 소녀와 결혼시키게 되면 3번 왕자가 결혼할 수 없게 됩니다
그러므로 2번 왕자는 2번 소녀와 결혼시킵니다
그러면 3번 왕자는 3번 소녀와 결혼하게 됩니다
그리고나서 보면 4번 왕자는 3~5번 소녀를,
5번 왕자는 4, 5번 소녀를 좋아하고 있으므로 (4, 4) - (5, 5) 나 (4, 5) - (5, 4) 로 결혼시킬 수 있습니다
따라서 이 경우엔
(1, 1) - (2, 2) - (3, 3) - (4, 4) - (5, 5) 또는 (1, 1) - (2, 2) - (3, 3) - (4, 5) - (5, 4) 의 두가지 경우가 가능합니다
다음,
1번 왕자를 2번 소녀와 결혼시킵니다
그러면 2번 왕자는 3번 소녀와 결혼하게 됩니다
그러면 3번 왕자는 1번 소녀와 결혼하게 됩니다
4번 왕자와 5번 왕자는 위의 경우와 같은 꼴이므로 이 경우에는
(1, 2) - (2, 3) - (3, 1) - (4, 4) - (5, 5) 또는 (1, 2) - (2, 3) - (3, 1) - (4, 5) - (5, 4) 의 두가지 경우가 가능해집니다
따라서 이번 케이스에서는 총 네가지 경우가 가능한데,
역시 어느 왕자도 결혼하지 않은 상태를 가정하면
1번 왕자는 1번 소녀나 2번 소녀를 선택할 수 있습니다
2번 왕자는 2번 소녀나 3번 소녀를 선택할 수 있습니다
3번 왕자는 1번 소녀나 3번 소녀를 선택할 수 있습니다
4번 왕자는 4번 소녀나 5번 소녀를 선택할 수 있습니다
5번 왕자도 4번 소녀나 5번 소녀를 선택할 수 있습니다
따라서 이 케이스의 출력 예시는
2 1 2
2 2 3
2 1 3
2 4 5
2 4 5
가 아닐까 예상해봅니다
세번째 케이스입니다

이 케이스는 총 여섯가지 경우가 가능한데,
말로 풀어쓰면 길어지므로 직접 종이에 끄적여보세요 :)
(1, 1) - (2, 2) - (3, 3) - (4, 5) - (5, 6) - (6, 4)
(1, 1) - (2, 4) - (3, 3) - (4, 5) - (5, 6) - (6, 2)
(1, 1) - (2, 6) - (3, 4) - (4, 5) - (5, 3) - (6, 2)
(1, 2) - (2, 4) - (3, 3) - (4, 5) - (5, 6) - (6, 1)
(1, 2) - (2, 6) - (3, 4) - (4, 5) - (5, 3) - (6, 1)
(1, 3) - (2, 2) - (3, 4) - (4, 5) - (5, 6) - (6, 1)
그렇다면 이 케이스의 출력 예시는
3 1 2 3
3 2 4 6
2 3 4
1 5
2 3 6
3 1 2 4
가 되는 것이 아닐까 생각합니다
-만,
환타님의 WA 소스는 이 세번째 케이스의 답이 제 생각과 다릅니다 =_=
※ 처음에도 언급했지만, 이 풀이는 'sparking의 번역본'을 보고 나름대로 의미를 생각해서 풀었기 때문에 실제 답과 같다는 보장은 없습니다 :(
'Solving process' 카테고리의 다른 글
| PKU [2234]. Matches Game. [WA] (10) | 2009.06.03 |
|---|---|
| 이걸 어떻게 구현해야 할 지 (1) | 2009.01.22 |
| PKU [1089]. Intervals. [TLE]. (2) | 2009.01.19 |
| Rush : Dlbo군의 Matrix Solution (8) | 2008.12.28 |
| 리턴군의 테스트케이스 의존성 코드가 먹혀들어간 이유. (4) | 2008.10.08 |