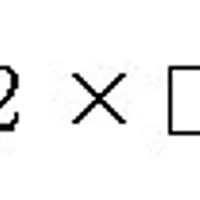안녕하십니까 Mr. K입니다
여기에 글을 쓰는것도 오랜만이군요 -_-;
원래 어제 올렸어야 되는데
수정된 ubint를 올려놓고 딴짓좀 하다보니 잊어버렸지 뭡니까;
그래서
공지를 띄우고 며칠 더 있다 올릴까, 지금 올릴까
하다가 지금 올립니다 -_-;
이번 포스트는 역행렬에 대해서 얘기해보겠습니다
이전까지 우리는
행렬의 기본적인 정의, 행렬간 덧셈·뺄셈의 정의, 행렬간 곱셈의 정의
등을 배웠습니다
행렬은 나눗셈의 개념은 없지만, 역행렬이라는 것이 있습니다
실수를 다룰 때, 다음과 같은 관계에서 a가 0이 아니라면 x, 즉 a의 역수를 생각해볼 수 있습니다

마찬가지로 행렬에서도,
다음과 같은 관계를 만족하는 행렬 A에 대해서는 X, 즉 A의 역행렬을 생각해볼 수 있습니다

[그림 2] A와 X 사이에 교환법칙이 성립해야하므로
A와 X는 모두 정사각행렬이다
그리고
A가 어떤 조건을 만족하여 역행렬이 존재함을 알게 된다면, 우리는 그 역행렬을 다음과 같이 표기합니다

[그림 3] 읽을 때는 A inverse라고 읽으면 됩니다
다른 행렬 B가 있을 때 그 역행렬이 존재한다면, B의 역행렬은 B inverse라고 읽으면 됩니다
그럼 이제, 간단한 예제를 가지고 역행렬을 직접 구해보도록 하겠습니다

어떤 행렬이 역행렬을 가지게 될 조건은 잠시 후에 언급하기로 하고, A의 역행렬을 구해봅시다
이 경우 역행렬이 존재하므로, ( 일부러 존재하는 case를 선택함 )
그림 2( AX = XA = E )의 관계를 만족하는 행렬 X를 구해보면 됩니다
그래서 A의 역행렬을 다음과 같이 놓으면, 그림의 두번째 줄에 있는 식이 성립합니다

[그림 5]
그럼 먼저,
A를 왼쪽에, A의 역행렬을 오른쪽에 곱한 것을 계산해보면 다음과 같습니다

마찬가지로
A의 역행렬을 왼쪽에, A를 오른쪽에 곱한 것을 계산해보면 다음과 같습니다

이렇게 구한 A의 역행렬은 그림 5의 두번째 줄에 있는 식을 만족합니다 ( 검산은 직접 :D )
하지만 행렬도 역행렬이 존재하지 않는 놈들이 있습니다, 마치 0의 역수가 존재하지 않는 것처럼
다음과 같은 행렬은 역행렬이 존재하지 않지요

그럼 이쯤에서 역행렬을 가지게 될 조건에 대해 봅시다
원래는 A의 원소를 임의로 정해놓고 역행렬을 구하는 과정을 보여드리면서 조건에 대해 얘기해야 하지만,
귀찮으니까 공식을 통해 보도록 하겠습니다 -_-;

네, 위 그림의 두번째 줄을 천천히 읽어보시면 조건이 나와있습니다
A의 원소를 1행 1열부터 각각 a, b, c, d라고 했을 때, ad-bc가 0이면 안되는거죠
이 때, ad-bc를 행렬식( determinant )이라고 하고 줄여서 D로 쓰곤 합니다
( 대학에 가서 선형대수학을 배우게 되면 D는 행렬식 대신 다른 의미를 갖게 되는데, 여기서는 일단 패스 )
그럼 이제 아까의 문제를 되돌아봅시다
조건같은 것을 생각하지 않고 다짜고짜 역행렬을 구했던 녀석은 D를 계산해보면 1×1 - 0×2 = 1이 나옵니다
그러면 공식에 의해서 역행렬을 구할 수 있지요, 물론 직접 계산해도 됩니다 :)
그리고 조건을 언급하기 직전에
역행렬이 존재하지 않는다고 했던 녀석은 D를 계산해보면 1×4 - 2×2 = 0이 나옵니다
그래서 이녀석은 역행렬을 구할 수 없습니다
다음 포스트에서는 행렬을 가지고 연립방정식을 푸는 것에 대해 언급할 것인데,
이처럼 역행렬이 없는 녀석들은 연립방정식의 해가 없거나 무한히 있거나 둘 중 하나가 되곤 하지요
뭐 어쨌든, 이제 역행렬의 성질에 대해 알아보겠습니다
첫째로, 역행렬의 역행렬은 자기 자신이 됩니다

위 그림을 보시면 A의 역행렬은 A inverse지만, 반대로 생각하면 A inverse의 역행렬이 A이기도 합니다

[그림 11] 마치 음수의 음수가 양수이듯이,
혹은 역수의 역수가 자신이듯이
둘째로,
각각 역행렬이 존재하는 두 행렬 A, B의 곱의 역행렬은 존재하고, 그것은 각각의 역행렬을 역순으로 곱해놓은 것과 같습니다

[그림 12] ∃는 exist라는 의미의 기호, 아마 고등학교 과정에서는 볼 일이 없을 것
다만, A와 B의 곱이 존재하기 위해서는 A와 B가 같은 꼴의 행렬이어야 한다는 것은 말하지 않아도 되겠지요?

[그림 13] AB와 그것의 역행렬로 추정되는 것과의 곱
곱의 결과가 단위행렬이 되므로 역행렬이 맞다
마찬가지로, BA의 역행렬이 존재한다면 (BA inverse) = (A inverse)×(B inverse)
마지막으로, 지수에 관한 성질도 한가지 있는데
A가 역행렬이 존재한다면, A의 거듭제곱의 역행렬은 A의 역행렬의 거듭제곱과 같습니다

[그림 14] 두번째 줄의 식은 k가 1일 때는 당연하다
이제, 역행렬에 관한 예제 하나를 풀어보고 이번 포스트를 마치도록 하겠습니다

위의 식을 만족하는 X를 구하면 됩니다
X의 왼쪽에 곱해진 행렬을 A라 하면, A의 행렬식은 0이 아니므로 역행렬을 구할 수 있습니다
그래서 양변의 왼쪽에* A의 역행렬을 곱해줍니다
*양변의 왼쪽에 : 행렬은 일반적으로 교환법칙이 성립하지 않으므로 왼쪽에 곱하는 것과 오른쪽에 곱하는 것의 결과가 각각 다른데, 위에서는 X와 A 사이에 교환법칙이 성립하는지의 여부를 알 수 없으므로 A의 역행렬을 오른쪽에 곱하게 되면 문제만 복잡해진다
그리고 다음과 같이 계산하면 됩니다

참 쉽죠? :D
이번 포스트는 여기까지입니다
다음번에는 연립일차방정식과 행렬에 관해 얘기하겠습니다 (__)
(포스팅 소요시간 : 약 90분)
'(비정기) Mr.K's Post > Weekly paper' 카테고리의 다른 글
| Matrix : Part 5 (0) | 2009.03.14 |
|---|---|
| [Bigfloat 지원사격?] 자연수부터 해봅시다 :) (4) | 2009.02.26 |
| Matrix : Part 3 (0) | 2009.02.09 |
| Matrix : Part 2 (2) | 2009.01.24 |
| Matrix : Part 1 (8) | 2009.01.17 |