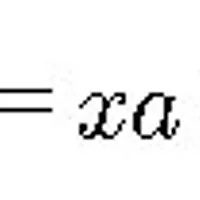안녕하십니까 Mr. K입니다
어제 저녁 내내 친구와 놀고 늦게 들어온 덕분에
포스팅하다가 피로를 이기지 못하고 자고 씁니다 -_-;
시작할게요!
여러분은 다음과 같은 식을 보면 □를 구할 수 있습니까?

[그림 1]
아마 중학교를 졸업한 수준의 학생들이라면 대부분 답을 구할 수 있을 것입니다 ( 답은 1이죠 )
이제 위 그림의 □를 x로 바꿔보겠습니다

[그림 2]
이제 이것을 방정식이라고 부를 수 있을 것입니다
( 사실 그림1, 2 모두 방정식이지만, 그림1과 같은 식을 통해서 배울 때는 방정식이라는 말을 보지 못했을 수도 있으므로 )
미지수 x의 차수가 1이므로 이것은 일차방정식입니다
이런 일차방정식이 두 개 이상 묶여있는 경우엔
그것을 연립일차방정식( 이하 연립방정식이라고 하겠습니다 )라고 합니다 ( 앞의 연립은 '연립주택'의 연립 )
다음 연립방정식에서 x와 y를 구할 수 있습니까?

답은 x = 1, y = 1입니다
첫째줄의 식에서 둘째줄의 식을 빼면 y의 값이 구해지고, 그 y의 값을 둘 중 아무데나 대입하면 x의 값이 구해집니다
푸는 방법이 왜 그런지 이해하지 못할 수 있지만, 어쨌든 답을 쉽게 구할 수 있습니다
그러면,
다음과 같은 연립방정식에서도 미지수 x와 y의 값을 쉽게 구할 수 있을까요?

사실 쉽습니다만 -_-; 복잡하다고 생각해보죠
이런 연립방정식은 다음 그림처럼 행렬의 곱으로 바꿔서 생각할 수 있습니다

그러면 눈에 보이시나요?
AX = B 꼴의 식이므로 양변의 왼쪽에 A의 역행렬( 존재한다면 )을 곱해주기만 하면 미지수의 값을 쉽게 구할 수 있습니다 :D
이 때, 이런 A를 연립방정식의 계수행렬이라고 합니다
한번 해볼까요?
우선, 계수행렬을 {3 4; 8 7}이라 하면 이것의 행렬식은 -11입니다
따라서 역행렬이 존재하겠지요
그러면 다음과 같은 과정을 거쳐서 x와 y를 구할 수 있습니다 :)

그런데, 과연 이 방법을 모든 연립방정식에 적용할 수 있을 것인가? 하면
그것도 아닙니다
역행렬이 존재하지 않는 녀석들이 있기 때문에
그런 계수행렬과 대응되는 연립방정식은 다른 방법으로 해결을 해야 합니다
아래의 두 케이스를 보시면,

[그림 7]

[그림 8]
두 케이스 모두 계수행렬의 역행렬을 구할 수 없습니다
이 때, 역행렬을 구할 수 없다는 것은
연립방정식의 첫째줄의 식의 양변에 적당한 수를 곱하면 둘째줄의 식의 좌변( 미지수 )을 0으로 만들 수 있음을 의미합니다
( 이것은 나중에 미지수의 개수가 많아지면 조금 더 엄밀하게 정의가 되겠지만, 지금은 기초적인 것을 얘기하고 있으므로 패스합니다 )
무슨 말이냐면,
그림 7의 연립방정식은 첫번째 줄에 17을 곱해서 두번째 줄을 빼버리면 다음과 같이 됩니다

마찬가지로, 그림 8의 연립방정식은 첫번째 줄에 17을 곱해서 두번째 줄을 빼버리면 다음과 같이 됩니다

모순이 등장했지요?
이렇게 판정하면 됩니다
계수행렬의 역행렬이 존재하지 않는 케이스의 경우,
( 미지수가 2개일 때는 ) 한 줄의 식이 다른 줄의 식의 배수가 되므로 위에서 한것처럼 빼보면
빼진 줄의 식이 0 = 0이 되거나 0 = k이 됩니다 ( k는 0이 아닌 실수 )
0 = 0이 되면 주어진 연립방정식을 참이 되게 하는 x, y의 개수는 무한하고,
0 = k가 되면 주어진 연립방정식을 참이 되게 하는 x, y는 없습니다
미지수가 3개 이상일 때도 계수행렬을 이용해서 푸는 방법이 많이 쓰이는데,
그것은 여기서 언급하지 않고 넘어가기로 하겠습니다
여기까지가 행렬의 기본입니다
심화된 부분을 더 포스팅할지 말지는 생각해보고 결정하도록 하겠습니다 =_=
(포스팅 소요시간 : 약 75분)
'(비정기) Mr.K's Post > Weekly paper' 카테고리의 다른 글
| Matrix : Part 4 (0) | 2009.03.06 |
|---|---|
| [Bigfloat 지원사격?] 자연수부터 해봅시다 :) (4) | 2009.02.26 |
| Matrix : Part 3 (0) | 2009.02.09 |
| Matrix : Part 2 (2) | 2009.01.24 |
| Matrix : Part 1 (8) | 2009.01.17 |