N(10만 이하의 자연수)마리의 소가 K(1만 이하의 자연수)가지의 품종을 가지고 있다
그 N마리 소들의 품종을 수열로 나열해놓자
그러면 이 소수열(cow수열)에서 부분수열(연속하지 않아도 됨)을 찾을 수 있다
이 때, 1~K의 수들로 이루어진 임의의 수열 중 소수열의 부분수열이 아닌 것들이 있을 것이다
그러한 수열들 중 길이가 제일 짧은 수열의 길이를 출력하시오
―가 이 문제의 내용입니다 =_=
문제의 입출력 예시를 보면
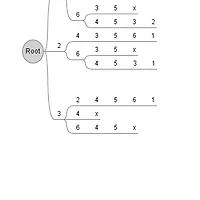
[입력: 편의상 수열을 가로로 나열했습니다]
14 5
1 5 3 2 5 1 3 4 4 2 5 1 2 3
[출력]
3
입니다
힌트에도 버젓이 나와있습니다만,
영어를 잘 모르는 탓에 처음 문제가 올라왔을 땐 제대로 읽지도 않았는데요 -_-; 오늘(24일)은 유독 눈에 들어오더라구요
위 수열에서 단항(원문과 비교하자면 single digit)으로 이루어진 수열은 [1], [2], [3], [4], [5]가 모두 존재합니다
그리고 이항(two digit)으로 이루어진 25개의 수열 [1,1], [1,2], [1,3], [1,4], [1,5], [2,1], …, [5,4], [5,5]들도 모두 위의 소수열에서 찾아낼 수 있습니다
그러면 출력값이 3인 만큼,
삼항으로 이루어진 수열 중에서는 소수열의 부분수열이 아닌 것들도 있겠구나 하시겠지요
힌트 끝부분을 보시면 [2,2,4]는 찾을 수 없다고 쓰여있습니다
----------------
간단한 예시를 하나 들어봅시다
7 3
1 2 3 2 1 3 2
이 경우에도 출력값은 3이 나옵니다, 가장 간단하게 생각해서 [1,1,1]을 찾을 수 없기 때문인데요
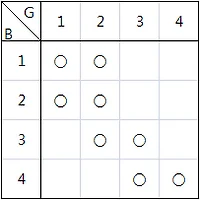
개인적으로는 이것을 matrix에 대응시켜서 풀었습니다
단항 수열의 경우 1×3 matrix를 이용하였고,
(소수열 안에 [1], [2], [3]이 존재할 경우 각각의 위치에 true 대입)

이항 수열의 경우 3×3 matrix, 삼항 수열의 경우 3×3×3 matrix(?)를 이용하였습니다


3항 수열의 경우 [1,1,1], [2,1,1], [3,1,1], [3,3,1], [3,3,3]을 찾을 수 없다
이 방법의 경우 최대 [N/K]+1 차원까지 계산해야하기 때문에
시각적으로 형상화할 수 있는 것은 3항 수열(3차원, 큐브형태)까지입니다
(붉은색 대괄호는 가우스기호(고등학교과정)입니다)
최대 [N/K]+1 차원이라는 말은
다시 말하자면 출력값의 최대값이 [N/K]+1 정도 된다는 말과 같습니다 (거의 정확합니다)
-------------
이렇게 풀었는데도 TLE가 나온 이유를 살펴보자면
N과 K가 적당히 크고, 품종의 분포가 고를 경우 가장 시간이 오래 걸립니다
입출력 예시의 경우가 그 한 예라고 볼 수 있습니다
N = 14, K = 5 이므로 최대 차수는 [14/5]+1 = 3 이고, 이것은 곧
최대 5^1 + 5^2 + 5^3 = 155 번의 탐색을 하고 나서야 답이 나오게 됩니다
그럼 이제, N과 K가 적당히 크고 품종의 분포가 고를 경우를 가정해봅시다
N = 30000, K = 50, 각 품종당 600마리씩 존재
이 경우 최소 50^1 + 50^2 + 50^3 + … + 50^600 + 1 = ??? 번의 탐색을 하고 나서야 답이 나오게 되므로 당연히 TLE입니다
아.. 이래서 TLE였구나 -_-;;
'Solving process' 카테고리의 다른 글
| UVa 341 진행상황 (0) | 2010.08.14 |
|---|---|
| PKU [2234]. Matches Game. [WA] (10) | 2009.06.03 |
| 이걸 어떻게 구현해야 할 지 (1) | 2009.01.22 |
| [PKU 1904. King's Quest] 문제해석 (12) | 2009.01.21 |
| PKU [1089]. Intervals. [TLE]. (2) | 2009.01.19 |