 그래프(Graph) - 그래프??
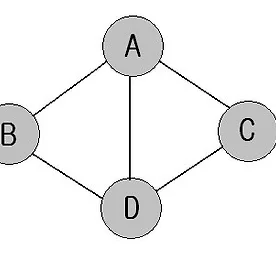
안녕하세요~ 오늘 이 시간에는 그래프에 대해서 알아볼까 합니다. 음 그래프란 무엇일까요? 그래프란 유한 개의 정점(V(G))과 유한개의 간선(E(G)) 구성된 집합입니다. 간선의 집합은 공집합일수도 있습니다. 즉 정점의 경우 하나도 존재하지 않는 그래프는 없지만 간선이 존재하지 않는 그래프는 존재할 수 있습니다. 예를 들어 이런 그래프가 있다고 한다면 각각의 점이라고 할수 있는 A, B, C, D는 정점이고, 이의 연결선이 간선입니다. V(G) = {A, B, C, D} E(G) = {(A,B), (A,C), (A,D), (B,D), (C,D)} 라고 할 수 있습니다. 또한 왼쪽의 경우 그래프라 할 수 있지만 오른쪽은 그래프라 할 수 없는것이지요. 그래프에는 방향성을 가지느냐 가지지 않느냐로 방향성 그래..
더보기
그래프(Graph) - 그래프??
안녕하세요~ 오늘 이 시간에는 그래프에 대해서 알아볼까 합니다. 음 그래프란 무엇일까요? 그래프란 유한 개의 정점(V(G))과 유한개의 간선(E(G)) 구성된 집합입니다. 간선의 집합은 공집합일수도 있습니다. 즉 정점의 경우 하나도 존재하지 않는 그래프는 없지만 간선이 존재하지 않는 그래프는 존재할 수 있습니다. 예를 들어 이런 그래프가 있다고 한다면 각각의 점이라고 할수 있는 A, B, C, D는 정점이고, 이의 연결선이 간선입니다. V(G) = {A, B, C, D} E(G) = {(A,B), (A,C), (A,D), (B,D), (C,D)} 라고 할 수 있습니다. 또한 왼쪽의 경우 그래프라 할 수 있지만 오른쪽은 그래프라 할 수 없는것이지요. 그래프에는 방향성을 가지느냐 가지지 않느냐로 방향성 그래..
더보기