본문 바로가기

Solving process

UVa 341 진행상황 뭐, 그냥 말로만 풀고있다고 하는 것보다야 직접 보여주는게 낫겠다 싶어서 -_-a 보다시피 3번째 케이스에서 제대로 된 답이 안나오고 있음// 경로 탐색 방식상 3번째 케이스처럼 양방향 길이 존재하는 경우에 대한 처리가 아직 잘 안되고있음 :( 더보기
[PKU 1989. The Cow Lineup] 문제해석 N(10만 이하의 자연수)마리의 소가 K(1만 이하의 자연수)가지의 품종을 가지고 있다 그 N마리 소들의 품종을 수열로 나열해놓자 그러면 이 소수열(cow수열)에서 부분수열(연속하지 않아도 됨)을 찾을 수 있다 이 때, 1~K의 수들로 이루어진 임의의 수열 중 소수열의 부분수열이 아닌 것들이 있을 것이다 그러한 수열들 중 길이가 제일 짧은 수열의 길이를 출력하시오 ―가 이 문제의 내용입니다 =_= 문제의 입출력 예시를 보면 [입력: 편의상 수열을 가로로 나열했습니다] 14 5 1 5 3 2 5 1 3 4 4 2 5 1 2 3 [출력] 3 입니다 힌트에도 버젓이 나와있습니다만, 영어를 잘 모르는 탓에 처음 문제가 올라왔을 땐 제대로 읽지도 않았는데요 -_-; 오늘(24일)은 유독 눈에 들어오더라구요 위 수.. 더보기
PKU [2234]. Matches Game. [WA] #include int main() { int maximum_cnt; int temp; int _register; while(scanf("%d", &maximum_cnt) != EOF) { _register = maximum_cnt; while(maximum_cnt--) { scanf("%d", &temp); } if(_register % 2 == 0) { printf("No\n"); } else { printf("Yes\n"); } } return 0; } WA 입니다. 님 게임(Nim Game) 의 일종인 것 같습니다만, 이 문제는 가져올 수 있는 갯수의 제한이 최대 쌓여진 뭉치의 갯수더군요. 그래서 간단하게 '뭉치의 갯수가 짝수이면 첫번째 플레이어는 이길 수 없는 거고, 홀수라면 이기겠다.' ..... 더보기
이걸 어떻게 구현해야 할 지 세 번째 케이스 6 3 1 2 3 3 2 4 6 2 3 4 1 5 2 3 6 4 1 2 4 5 //1 2 3 5 6 4 3 1 2 3 3 2 4 6 2 3 4 1 5 2 3 6 3 1 2 4 이 방법이 맞지요? 더보기
[PKU 1904. King's Quest] 문제해석 안녕하십니까 Mr. K입니다 다들 이번 문제에 대해 혼란스러워하는 것 같아서 일단 제가 해석한 대로 전개해보겠습니다 친구와 약간의 음주를 하고 와서 쓰는 것이라 약간 말이 안되어보이는 것이 있을지도 모르겠습니다만 그냥 쓰겠습니다 문제의 입력 예시를 보면 4 2 1 2 2 1 2 2 2 3 2 3 4 1 2 3 4 라고 되어있는데, 여기서 마지막줄의 "1 2 3 4", 즉 '마법사가 만들었던 원래의 결과물'은 무시하기로 합니다 (왜 우리가 output으로 나와야 하는 한가지 경우의 수를 input으로 넣어야 하는지에 대한 의문도 잠시 접어두기로 하고) 그리고나서 2 1 2 2 1 2 2 2 3 2 3 4 를 보면, 첫번째 왕자는 2명의 소녀를 좋아하고, 그 소녀의 번호는 각각 1과 2입니다 두번째 왕자는 .. 더보기
PKU [1089]. Intervals. [TLE]. #include typedef struct { int initial; int final; } closed_interval; closed_interval input[50000]; int main() { int case_cnt, i, j; int case_max, case_min; scanf("%d", &case_cnt); for(i=0 ; i=1 ; i--) { for(j=1 ; j input[j].initial) { input[j-1].initial ^= input[j].initial; input[j].initial ^= input[j-1].initial; input[j-1].initial ^= input[j].initial;.. 더보기
Rush : Dlbo군의 Matrix Solution 네, 논란이 많았죠, Matrix 류엔트군은 술마시고 코딩해서 기억이 안난다고 하질 않나 Dlbo군은 류엔트군의 풀이와 99% 같은 코드를 올리고는 미리 풀긴 했는데 정리를 못한 상태에서 류엔트군의 AC가 올라오니까 그걸 보고 자기 풀이의 군더더기를 뺐다고 하질 않나 (사실 물증이 없어서 아직도 1%정도 의심은 가지만, 여기선 그걸 추궁하는게 아니니까 그냥 믿고 넘어갑니다) 그것 때문에 제가 뭔가 납득이 갈 만한 풀이를 올려달라고 했고, 얼마 전에 Dlbo군이 솔루션을 올려주었지요 솔루션을 읽고나서 알고리즘을 직접 적용해보니 아주 정확히 답이 떨어집니다 알고리즘의 목적( M번째 작은 값을 K라 가정하고, K보다 작은 값을 가지는 행렬상의 원소의 개수를 counting하는 것 )도 꽤나 깔끔하고, 합리적이.. 더보기
리턴군의 테스트케이스 의존성 코드가 먹혀들어간 이유. http://ko.wikipedia.org/wiki/%EB%B0%80%EB%9F%AC-%EB%9D%BC%EB%B9%88_%EC%86%8C%EC%88%98%ED%8C%90%EB%B3%84%EB%B2%95 밀러-라빈 소수판정법에 관한 위키페디아의 링크입니다. 참 난감...한 소수판정법이긴 합니다. "이건 일단 합성수다!"라고 판정은 할 수 있지만, "이거 소수인거 같긴 한데..."라니 원 ㄱ-;; 우리가 풀었던 factovisor에서도 순수하게 그냥 소수로 쌩 때리면 풀기 힘든만큼, 테스트케이스에서 약간의 여유를 부려 밀러-라빈 소수판정법으로 풀 수 있게 해둔것 같습니다. 리턴군, 환타님, 저 세명의 코드에 대한 테스트케이스들의 결과로 보컨데 예상되는 형태의 테스트케이스들은 모두 밀러-라빈 소수판정법에 의해.. 더보기
규칙을 찾아봅시다 Reuent님의 소스로 행X행의 행렬에서 열(A,B,C...AX)번째 원소를 정리해봤습니다. 규칙이 보이시나요? 전 안보여요 ㅜㅜㅜㅜㅜㅜㅜ 더보기
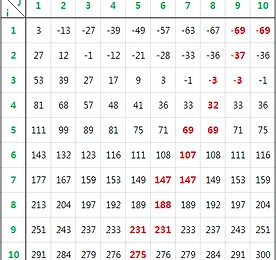
[PKU 3685. Matrix] 줄여서 생각해봅시다 우리가 문제에서 생각해야 하는 행렬의 최대 차수는 무려 5만차입니다 (여기서 말하는 차수는 행렬의 size를 의미합니다) 그리고 행렬 내의 i번째 행, j번째 열의 원소인 a_ij의 값은 i^2 + 100000*i + j^2 - 100000*j + i*j 이지요 (이하 a_ij는 (i, j)로 표기하겠습니다) 약간 고쳐서 간단히 만들면 (i+j)^2 - i*j + 100000*(i-j)가 됩니다 그런데 여태까지 ↘이 방향으로 오른쪽 위에서부터 왼쪽 아래까지 읽어내려오는 방식은 (즉, n차 행렬에 대해 (1, n), (1, n-1), (2, n), (1, n-2), (2, n-1), (3, n), (1, n-3), …, 이 순서로 읽어내려오는 ) 행렬의 차원이 커지면 저 순서로 읽을 수 없게 되고 말아버립.. 더보기
PKU 3685 발견사항 보고. 입력에 50000 1이랑 50000 2 넣어보세요. 기존 방식처럼 오른쪽 위에서부터 대각선 오른쪽 아래로 내려가는걸 반복하는 방식으로 풀었다면 두 입력에 대한 값이 같습니다. ㅡ.,ㅡ... 아래는 i를 1부터 5까지, j는 49996부터 5만까지 연산한 결과값입니다. -2499849987 -2499849993 -2499849997 (-2499849999 -2499849999) -2499699988 -2499699993 -2499699996 -2499699997 -2499699996 -2499549987 -2499549991 -2499549993 -2499549993 -2499549991 -2499399984 -2499399987 -2499399988 -2499399987 -2499399984 -24992.. 더보기
이번 문제.... 아직 AC 받은건 아닌듸요... 너무 피로해서 지금 죽을꺼 같아서 솔루션 만들어놓고도 코드로 못옮기고 있는데... 이거 확인해 보셨나요? 식이 i^2 + 100000i + j^2 - 100000j + ij 잖습니까... i만 1 증가시켜 비교해 보면... i^2 + 100000i + j^2 - 100000j +ij와 i^2 + 100000i + j^2 - 100000j +ij + 2i + j + 100001이 되어서 i 증가시 2i + j + 100001만큼 증가함을 알 수 있지요. j만 증가시켜도 그렇겠지요? (1,1)의 값이 3이니 굳이 저 연산 안하고 증감에 따른 차이만큼만 더해도 나와요. -_-; 더보기
행렬이 뭐에요???????????????????? 그냥 배열에 i*(i+100000)+j*(j-100000)+i*j 넣고 찾으면 되는건가요? 더보기
안돼~~~tree summing 왼쪽노드들만 검사하다니 #include int len; int run(int sum,int level) { int n=2,leaf=0,i=0; char ch; while(n--) { ch=getchar(); if(ch==')') return 1; if(ch=='(') { scanf("%d",&i); sum+=i; leaf+=run(sum,level+1); } } if(leaf==2/*&&sum==len*/) printf("%d ",sum); return 0; } main() { char tmp; scanf("%d",&len); tmp=getchar(); run(0,1); } 안친하던 재귀함수랑 좀 친해져보려고 재귀로 짜보긴 하는데요......... 어떤 처리를 더 해줘야 중간에서 안끝날까요? 하아........... 재귀랑은 .. 더보기
PKU 1145, UVa 112 Tree Summing 입력 샘플 22 (5(4(11(7()())(2()()))()) (8(13()())(4()(1()())))) 20 (5(4(11(7()())(2()()))()) (8(13()())(4()(1()())))) 10 (3 (2 (4 () () ) (8 () () ) ) (1 (6 () () ) (4 () () ) ) ) 5 () 0 () -1 (-1()()) 77 (77(1()())()) -77 (-77()()) -7 (1 (-6 (2 (1 ()()) (-4 ()(1 (1 ()())(-1 ()()) ) ) ) () ) () ) 0 () 3 (3 (4 (5 ()()) (8 (-3 (-7 ()())())(-4 ()(-8 ()())))) (6 (6 (-5 ()())(-6 ()(-9 ()())))(7 ()()))) 0 (1() .. 더보기
Tackle to Mr.K's Solution.(PKU 1145) #include #include #define SIZE 300 typedef enum storeType { NONE, NUMBER, LETTER, BRANCH, LEAF } storeType; typedef struct { int nPart; char cPart; storeType status; } card; /* status의 내용을 바꿔주는 것만으로 int형과 char형을 자유자재로 다룰 수 있어서 앞·뒤 뒤집는게 쉬운 card에 비유, 디버깅이 불편하다는 것이 단점 */ void main() { int searchKey; char inputStr[ SIZE ]; card adjusted[ SIZE ]; card stack[ SIZE ]; card temp[ SIZE ]; int compare = 0.. 더보기

티스토리툴바