안녕하십니까 Mr. K입니다
어제 그제 노느라 제대로 포스팅을 못했습니다 -_-;
오늘도
간이 나빠져서 입원하신 부친 병문안 다녀오는 일이 있어서 그냥 다음주로 미룰까 하다가
하루종일 병원에 있는 것도 아니고 해서 늦게나마 포스팅합니다/
지난번 포스트에도 Matrix에 대한 내용을 적어놓고 왜 또 이번에 Matrix를 다루는지 의아해 하실 분들이 있겠습니다만 (있나?)
이 팀블로그에서 하는 일이 주간 포스트만 있는 것이 아니지요,
바로
알고리즘 대회 기출문제.. 라고 생각되는 것들을 임의로 골라서 같이 풀어보고 토론(..)하는 일도 하고 있습니다만
번역되는 문제들을 보면 (혹은 개인적으로 문제 리스트를 훑어볼 때에도)
종종 문제 자체에서 Matrix를 이용하거나
Matrix를 이용해서 풀면 쉬울듯한,
그것도 아니라면 최소한 Matrix를 이용해서 알고리즘을 세우는 것 정도는 가능하게 되어있는 문제들이 있었습니다
다른 멤버들이야 다들 고졸 학력을 가지고 있으니까 그닥 상관없겠지만
환타님은 이제 곧 중졸 학력을 갖게 되지요 (아직 졸업식을 안했으니 현재는 초졸이라고 불러야 할수도 -_-;;)
그렇다보니, 예습을 하지 않았다면
Matrix, 즉 행렬에 관한 지식이 전무한 상태라
나머지 고졸 멤버들이 행렬을 이용해서 쉽게 알고리즘을 설계하는 동안
조금 더 머리를 싸매고 고민해야한다는 문제가 발생합니다
그래서 이번 포스트부터 한동안은 행렬의 기초부터 천천히 포스팅 할 생각입니다
시작할게요!
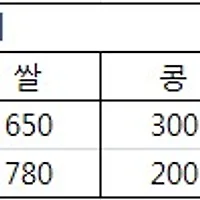
컴퓨터를 만드는 어느 회사는 두 공장에서 컴퓨터를 생산하고, 이것을 세 곳의 대리점으로 보낸 다음 판매한다고 한다. 이 때, 컴퓨터 한 대를 각 공장에서 각 대리점으로 운송하는 비용은 아래 표와 같다. 이 표를 보고 …


위의 글상자에서 운송 비용을 나타낸 표는 아래와 같이 숫자만을 묶어 나타낼 수 있습니다

이처럼 수를 직사각형 모양으로 배열하여 나타낸 것을 행렬( matrix )이라고 하고,
행렬을 이루는 각 수를 그 행렬의 성분( element )이라고 합니다.
행렬에서 성분의 가로배열을 행( row )이라고 하고, 위에서부터 차례로 제 1행, 제 2행, … 이라고 합니다
또, 성분의 세로배열을 열( column )이라고 하고, 왼쪽에서부터 차례로 제 1열, 제 2열, … 이라고 합니다

행의 수가 m, 열의 수가 n인 행렬을 m행 n열의 행렬 또는 m×n 행렬( m by n matrix )이라고 하고,
특별히 행의 수와 열의 수가 같은 행렬을 정사각행렬( square matrix )이라고 합니다
따라서 위 행렬은 2×3 행렬이고,
제 1행과 제 1열은 각각 아래의 그림과 같습니다

제 1행

제 1열
제 i행( i번째 행 )과 제 j열( j번째 열 )이 만나는 위치에 있는 성분을 (i, j)성분이라고 합니다
예를 들면, 위 행렬에서 (1, 2)성분은 2, (2, 1)성분은 2, (2, 3)성분은 3입니다
행렬은 흔히 아래와 같이 대문자를 사용해서 나타내곤 합니다

여기에 하나 덧붙이자면
환타님이 이 내용에 대해 모를것이다 가정하고 시작하긴 했지만, 아마 C를 공부했기 때문에 아실겁니다
바로 위의 그림과 아래의 코드가 같은 내용이라는 것을 -_-;
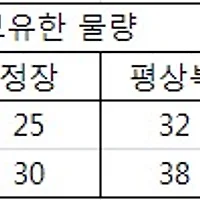
참고로, 직사각형 모양으로 배열된 자료는 여러가지 모양의 행렬로 나타낼 수 있습니다
아래의 표를 두 행렬 M, N으로 나타낸다고 하면 다음과 같은데,



이 때, 행렬 M의 1행은 영희의 국어, 수학, 영어 성적을 나타내고,
행렬 N의 1행은 영희와 철수의 국어 성적을 나타내게 됩니다
두 행렬 A와 B 각각의 행의 수, 열의 수가 같으면 두 행렬은 서로 같은 꼴의 행렬이라고 합니다
특별히, 두 행렬 A와 B가 서로 같을 꼴이면서 대응되는 성분이 각각 같을 때, 이 두 행렬은 서로 같다고 하고,
기호로는 A = B 로 나타냅니다

이번 포스트는 여기까지 쓰는 것으로 하고,
다음주에 행렬의 연산에 대해 쓰도록 하겠습니다
여유가 된다면 역행렬까지 언급할지도 모르겠네요
(포스팅 소요시간 : 약 85분)
'(비정기) Mr.K's Post > Weekly paper' 카테고리의 다른 글
| Matrix : Part 3 (0) | 2009.02.09 |
|---|---|
| Matrix : Part 2 (2) | 2009.01.24 |
| Matrix Decomposition (1) | 2009.01.08 |
| 무리수 √2의 값을 구해보자! : Part 5 (3) | 2008.12.27 |
| Interpolation : Part 3 (12) | 2008.12.05 |