안녕하세요 Mr. K입니다
사정이 좀 생겨서 아마 matrix의 포스팅이 끝나고나면 한동안 주간 포스트를 접어야 할지도 모르겠습니다;
(하지만 문제는 시간 나는대로 풀어서 올릴 예정)
오늘 다룰 내용은 행렬의 연산입니다
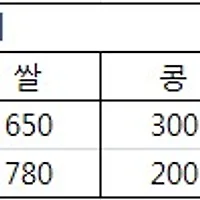
다음 표는 영희네 옷가게에서 어제까지 보유한 물량과 오늘 구입한 물량을 나타낸 것이다. 이 표를 보고 …




위의 글상자에서 어제까지 영희네 옷가게에서 보유한 물량과 오늘 구입한 물량을 각각 아래와 같이 행렬로 나타내기로 합니다

그러면 영희네 옷가게에서 현재 보유하고 있는 각 옷의 물량은 아래 표와 같습니다

이 때, 이 표의 성분은 A와 B의 대응하는 성분의 합이고, 이것을 행렬로 나타내면 다음과 같습니다

이처럼 행렬 A와 행렬 B의 대응하는 성분의 합을 성분으로 갖는 행렬을 A + B로 나타내고 A와 B의 합이라고 합니다
앞의 행렬 A, B에 대해서 A+B를 구하면 아래와 같습니다

일반적으로, 같은 꼴의 두 행렬의 덧셈은 다음과 같이 대응하는 성분의 합으로 정합니다

두 행렬이 같은 꼴이 아니라면 덧셈은 정의되지 않습니다
그러면 행렬의 덧셈은 수를 다룰 때와 마찬가지로 다음과 같은 교환법칙이나 결합법칙이 성립합니다
(증명은 관심있는 사람들만 직접 해보세요 :D)

위의 것이 교환법칙, 아래의 것이 결합법칙
아래와 같은 연산의 경우 괄호를 생략하기도
추가로, 성분이 모두 0인 행렬을 영행렬( zero matrix )이라고 합니다
예를 들면, 다음의 그림은 각각 1×2행렬, 2×1행렬, 2×2행렬, 2×3행렬인 영행렬입니다

영행렬은 행과 열의 크기에 관계없이 보통 대문자 o를 사용해서 나타냅니다
(관계가 없다기보다는, 보통 영행렬이 아닌 다른 행렬의 크기에 맞춰서 생각하곤 합니다)
그러면 이 영행렬은 임의의 행렬 A에 대해 다음을 만족합니다

덧셈이 있다면 뺄셈도 있어야겠지요?
아래와 같은 세 행렬에 대해

A + B = O가 성립한다면, B의 성분은 무엇이 되어야 할까요?
우리는 위에서 행렬의 덧셈을 다루었기 때문에, 그 과정은 자연스럽게 다음과 같이 이루어집니다

그리고
이전 포스트에서 행렬이 같을 조건에 대해 알았고,
수에 대한 사칙연산은 이미 알고 있으니 다음과 같은 과정이 이루어집니다

그러면 행렬 B의 각 성분은 행렬 A의 각 성분의 부호를 바꾼 것과 같아집니다
이제 임의의 행렬 A에 대해서,
A의 각 성분의 부호를 바꾼 것을 성분으로 갖는 행렬을 -A로 나타내기로 합니다
그러면, 임의의 행렬 A에 대해서 아래의 그림이 성립합니다

이제 같은 꼴의 A, B에 대하여 A + (-B)를 A - B로 나타내고, 이것을 A에서 B를 뺀 차라고 합니다

두 행렬이 같은 꼴이 아니라면 뺄셈도 정의되지 않습니다
다음은 행렬의 실수배에 대해서 보겠습니다
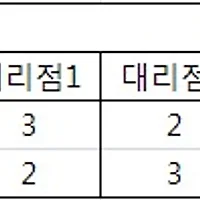
어느 도시의 현재 대중 교통 요금은 다음 표와 같다고 한다.

앞으로 10년 뒤에 이 도시의 대중 교통 요금은 현재 요금의 두 배가 된다고 할 때, 다음 물음에 …

앞으로 10년 뒤에 이 도시의 대중 교통 요금은 현재 요금의 두 배가 된다고 할 때, 다음 물음에 …
위의 글상자에 나온 표를 행렬로 쓰면 아래와 같습니다

그리고 10년 후의 요금은 각각 현재 요금의 두배이므로 이것을 행렬로 나타내면 아래와 같습니다

이제 M'과 M을 비교해보면
M'의 각 성분은 M의 각 성분을 2배한 것과 같음을 알 수 있습니다

이 때, 행렬 M'을 간단히 2M으로 나타내기로 합니다
일반적으로, 임의의 행렬 A의 각 성분에 임의의 실수 k를 곱한 것을 성분으로 갖는 행렬을
행렬 A의 k배라고 하고, 이것을 기호로 kA라 나타냅니다

여기서 R은 실수집합을 뜻한다
그러면 1A = A, (-1)A = -A, 0A = O, kO = O 가 자연스럽게 성립하게 되겠지요
행렬의 실수배에 대해서는 다음과 같은 법칙이 성립합니다

A, B는 같은 꼴의 행렬이고,
m, n은 임의의 실수이다
이번 포스트는 여기까지 쓰는 것으로 하겠습니다
행렬의 곱셈까지 설명하려고 했지만, 지금 이것도 (그림덕분에) 나름 스압이 쩔어서요 -_-;
아마 역행렬까지 언급할 수 있지 않을까 싶네요
(포스팅 소요시간 : 약 90분)
'(비정기) Mr.K's Post > Weekly paper' 카테고리의 다른 글
| [Bigfloat 지원사격?] 자연수부터 해봅시다 :) (4) | 2009.02.26 |
|---|---|
| Matrix : Part 3 (0) | 2009.02.09 |
| Matrix : Part 1 (8) | 2009.01.17 |
| Matrix Decomposition (1) | 2009.01.08 |
| 무리수 √2의 값을 구해보자! : Part 5 (3) | 2008.12.27 |